概述

该论文介绍了一种创新的方法，即通过自适应重构Merkle树来增强区块链的可扩展性。Merkle树是区块链体系结构的基本组成部分，负责确保数据完整性并促进高效的验证过程。传统的静态树结构存在可扩展性问题，尤其是当区块链网络需要处理大量的交易时。

论文提出了自适应的Merkle树模型，该模型可以基于使用模式动态调整树的配置，从而显著减少平均路径长度，降低计算开销。研究展示了适用于二叉和非二叉树的自适应重构方法，并通过基于以太坊区块链的实验验证了这种方法的有效性，结果表明与传统Merkle树相比，自适应Merkle树在重构初期的效率提升达到了30%以上。

方法

借鉴哈夫曼树的优化方法，将使用频率较低的数据放到路径较长的叶子节点中。

平衡的Merkle树的平均路径长度m表示每个节点允许的最大子节点数(度);

自适应Merkle树的平均路径长度反映了霍夫曼码的平均长度，计算为所有码长的加权和，对应符号的概率作为权重

p是第i个符号出现的概率，l是第i个符号的编码长度。

由香农熵公式，给定特定概率分布的霍夫曼码的理论最小平均长度为：

Δ表示路径长度与理论最小路径长度之差，Δ的绝对值越小表示路径长度越小，开销越小

示例

假设原来有两个叶子节点：

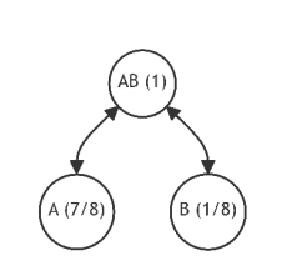
新加节点C分别与A、B计算出Δ：

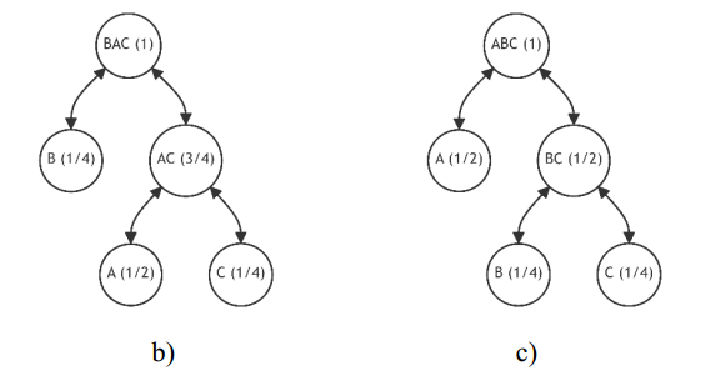
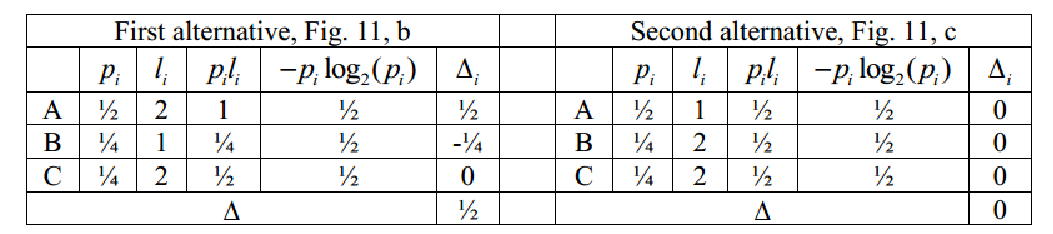
理想情况下，具有零差异(Δ= 0)的树结构即为最优结构。然而，这种理想的结构不一通过简单地向前面的配置添加叶子来实现，也就是说，单一对某个叶节点进行重构不一定能够达到Δ= 0。此时应该考虑交换叶子对。

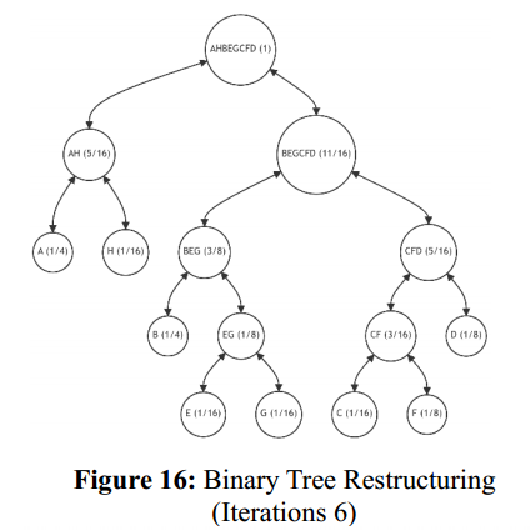
叶子B, F和H是交换位置的候选，产生三种选择:

交换B和H的位置之后重新计算Δ：

此时继续交换叶子H、F得到Δ=0。

此外该方法也对多叉树起作用

verkel树

解决merkle树验证时需要节点的Merkle路径的问题

在Merkle树中，验证需要提供从叶子节点到根节点的所有兄弟节点的哈希值，而在Verkle树中，验证者只需要提供由向量承诺生成的证明，这样可以大大减少证明的大小。

未来工作

优化merkle树重构算法